Karnaugh Maps (K-Maps)

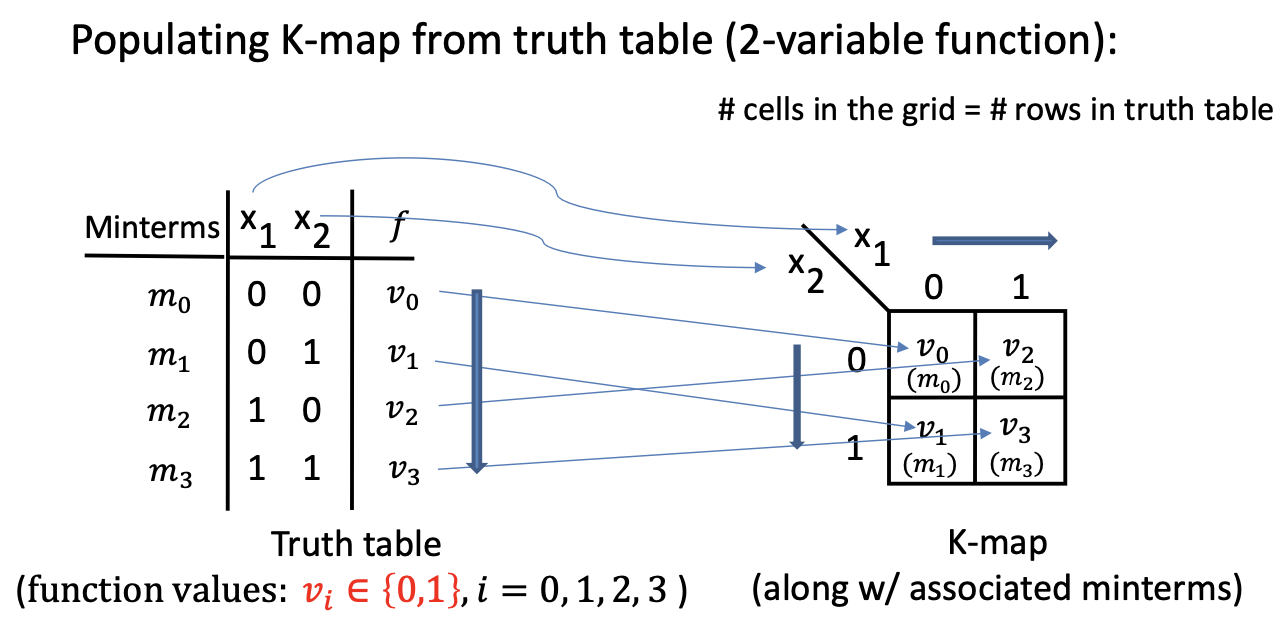
• A K-Map contains all the same information as truth table but in a different form
  • Truth table is “tabular”, K-map is arranged as a grid of squares or cells
  • The “coordinates” of a square represent the function’s input values
  • The content of any square is the function’s output value for the corresponding coordinates/inputs
  • The rows and columns of a K-map are labelled in a way so that only 1 variable changes between adjacent rows and columns

2-variable function §

Example:

Alternative Algebraic Explanation:

The green rectangles encompass 2 “1”s corresponding to $m_0+m_1$ yielding

$m_0+m_1=x_1^{\prime }{x}_2^{\prime }+x_1^{\prime }{x}_2=x_1^{\prime }$

Similarly the red rectangle encompasses 2 “1s” corresponding to $m_1+m_3$ yielding

$m_1+m_3=x_1^{\prime }{x}_2+x_1{x}_2=x_2$

Thus the expression that covers all the “1”s in the K-map is

$f=x_1^{\prime }+x_2$

SOP simplification using K-maps §

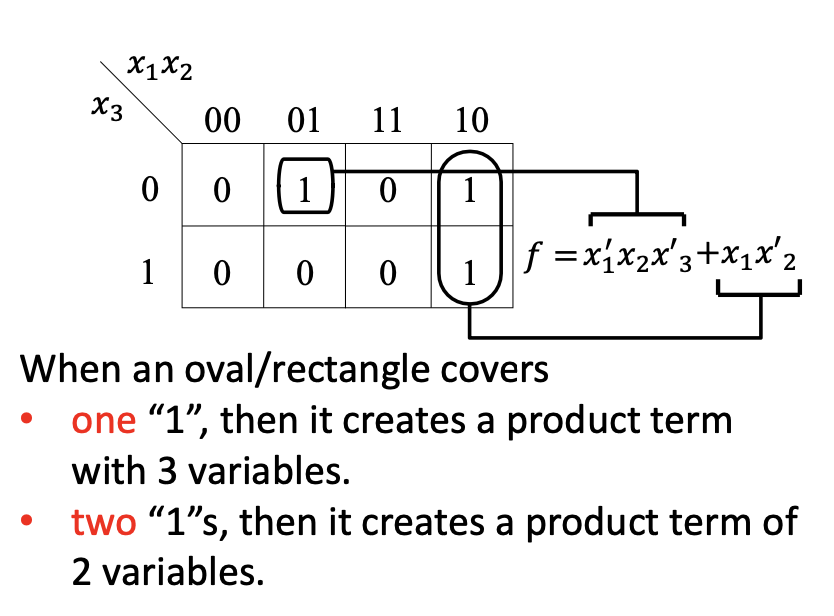
• For an SOP expression for the function, all “1“‘s in the K-map must be covered by one or more rectangles
• Find rectangles as large as possible covering “1”s noting that
  • it’s ok if a “1” is covered by more than 1 rectangle
  • the number of cells covered by a rectangle must be a power of 2, (e.g. $2^0,2,4,8,16$)
• For a low cost SOP expression, select as few rectangles as possible while ensuring to cover all of the “1”s in the K-map
• Possible to have multiple solutions that are equally as good

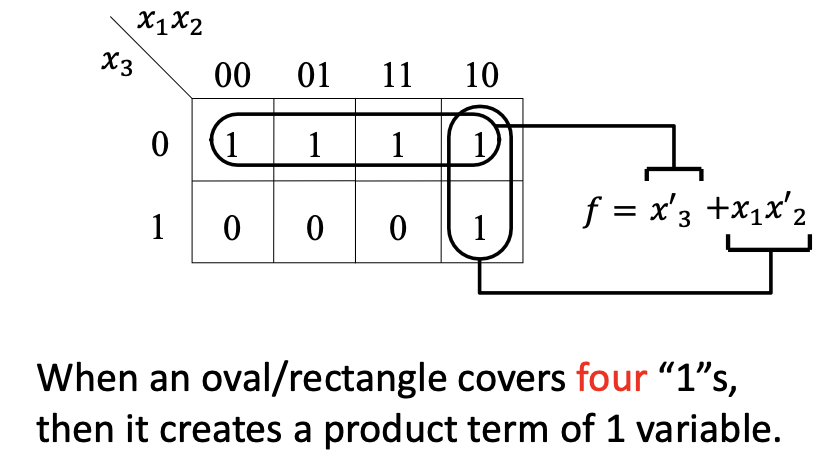
3-variable function §

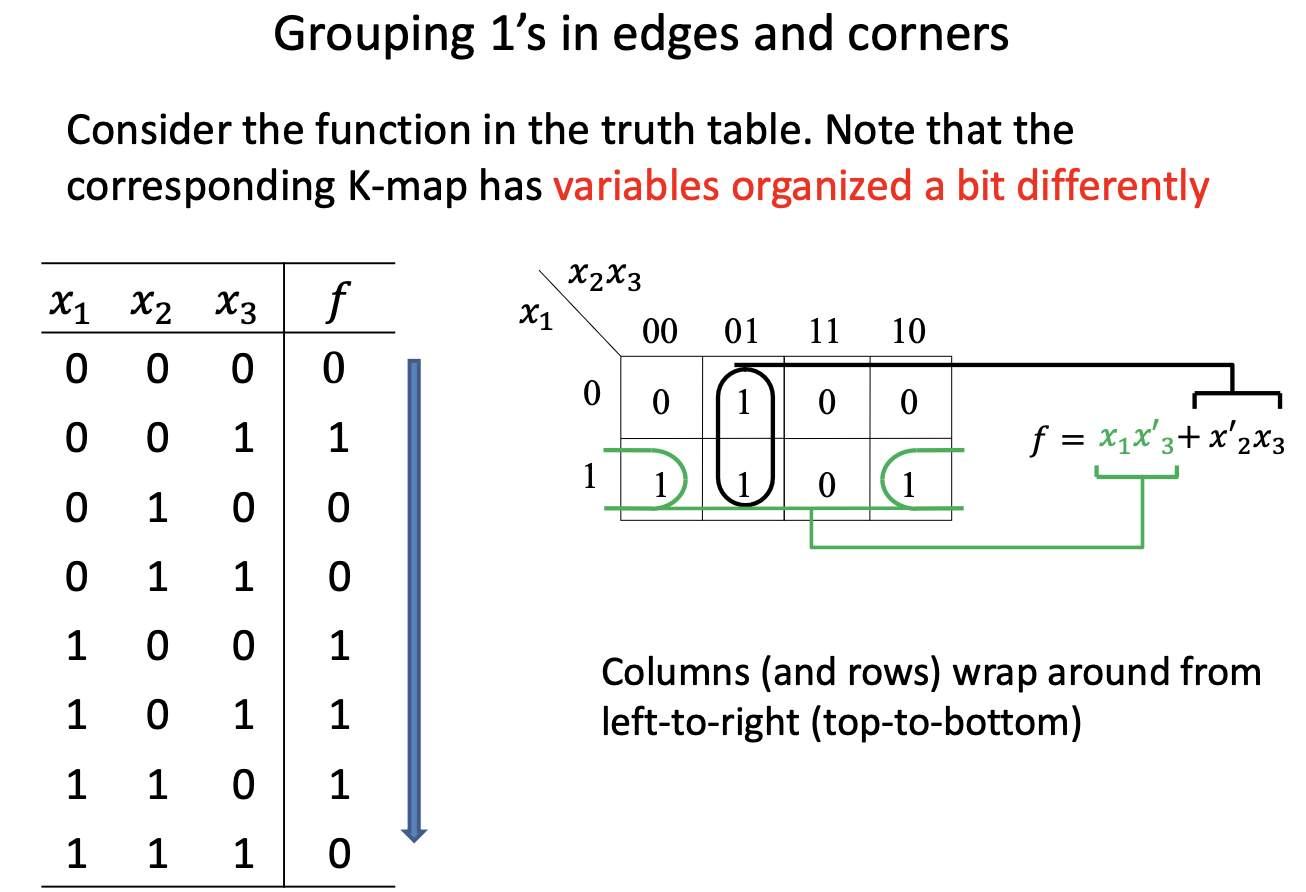
Grouping 1’s in edges and corners §

Remarks on K-map §

In general, for an n-variable function a rectangle/oval encompassing 1’s in

• 1 ($2^0$) square (i.e., cell) corresponds to a product term of n variables (i.e. minterm)
• 2 ($2^1$) adjacent squares correspond to a product of n - 1 variables
• 4 ($2^2$) adjacent squares correspond to a product of n - 2 variables
• 8 ($2^3$) adjacent squares correspond a product of n - 3 variables