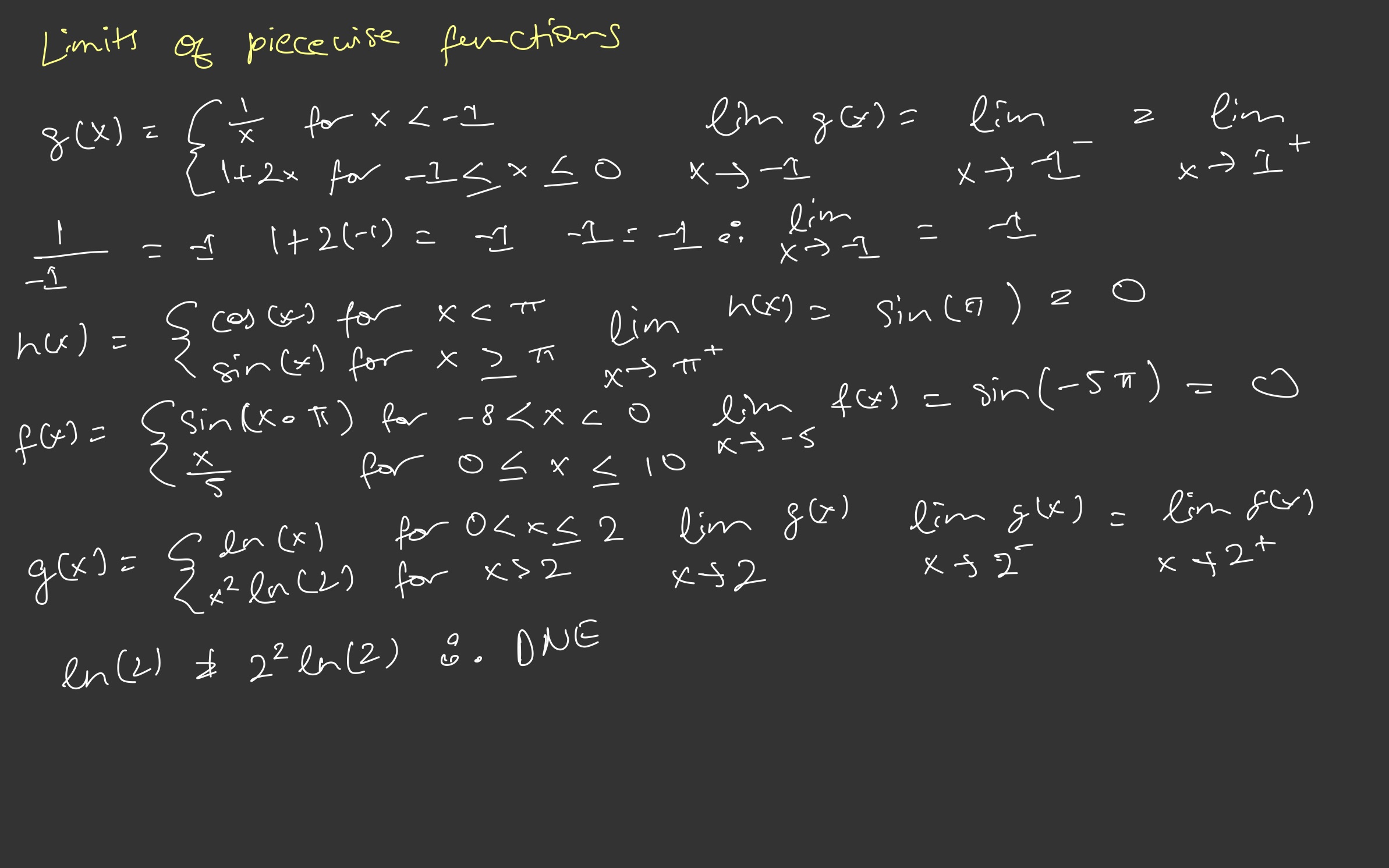Limits of piecewise functions

Limits of piecewise functions can differ from the direction we’re approaching them from

For example §

f(x) = $\{$ $\frac{x+2}{x-1}$ for 0 < x $\le$ 4 $\sqrt{x}$ for x > 4

lim f(x) = $\sqrt{4}$ as it’s approaching from the right side (4.001, 4.01) which is greater than 4 x -> 4${}^{+}$

lim f(x) = $\frac{4+2}{4-1}$ = $\frac{6}{3}$ = 2 as it’s approaching from the left side (3.99, 3.9) which is less than 4 x -> 4${}^{-}$

But what if x is approaching neither from left or right side §

If the limit approaching from left and the right side is the same then the limit exists

otherwise it doesn’t

Example:

lim f(x) = 2 x -> 4${}^{+}$

lim f(x) = 2 x -> 4${}^{-}$

Both left and right side equal 2 $\therefore$ the limit as x -> 4 is 2!

Worked Examples §