Matrix Multiplication

Properties of Matrix Multiplication §

[! Properties of Matrix Multiplication]

Let c $\in \mathbb{R}$ and A, B, C be matrices of appropriate sizes. Then:

a) IA = A | I is an identity matrix

b) AI = A | I is an identity matrix

c) A(BC) = (AB)C | Matrix multiplication is associative

d) A(B + C) = AB + AC | Left distributive law

e) (B + C)A = BA + CA | Right distributive law

f) (cA)B = c(AB) = A(cB)

g) (AB)${}^T$ = B${}^T$ A${}^T$

Pre-Requisite §

The column of matrix 1 being multiplied and the row of matrix 2 being multiplied have to be the same for this operation to even be possible Order matters AB $\ne$ BA

Rule §

Use the direction $\Rightarrow$ $\Downarrow$

Example §

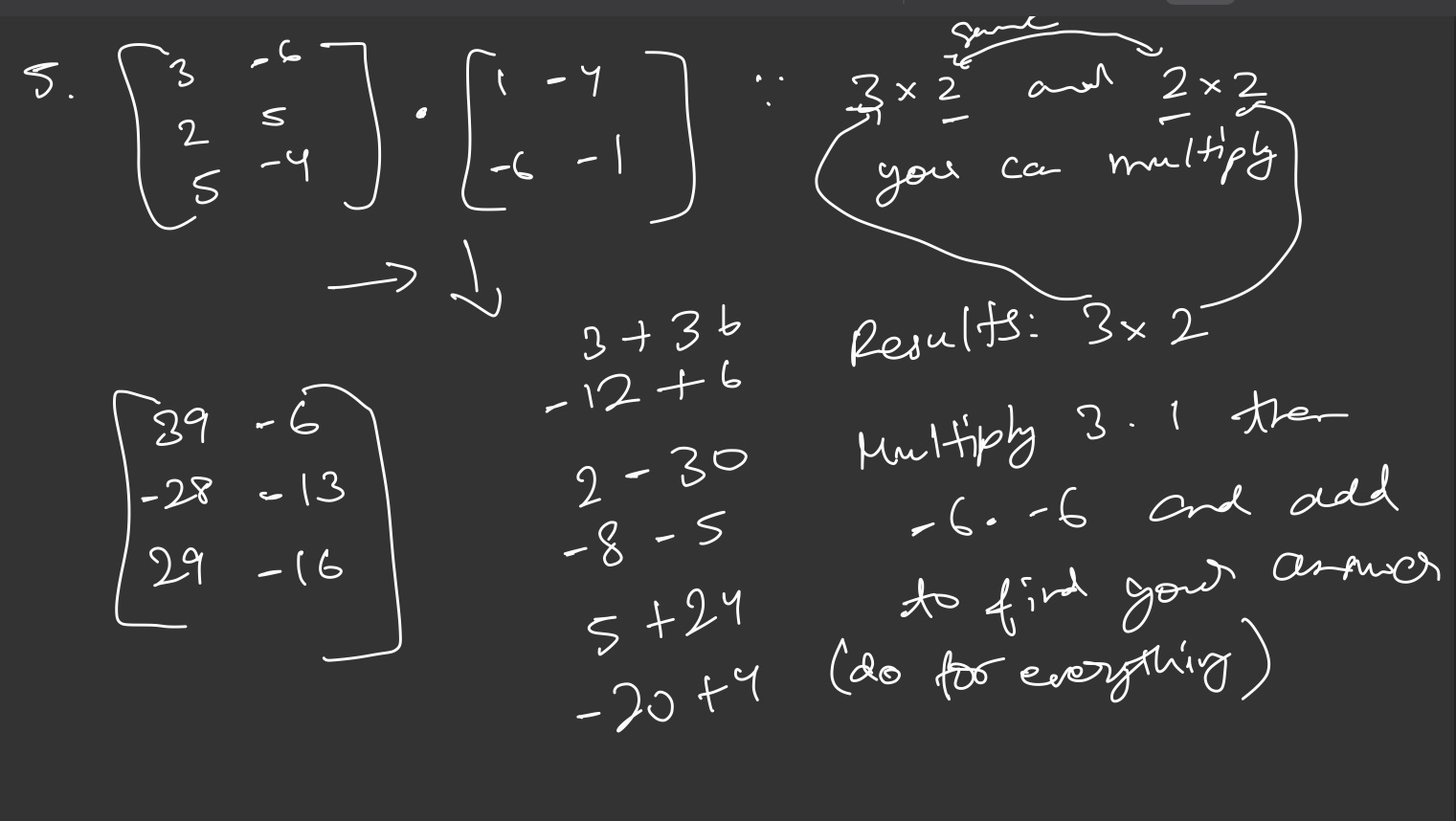
Result §

Results in a matrix with the row of the 1st matrix and the column of the 2nd matrix