lim f(g(x)) = f(lim g(x)) x -> a x -> a
The statement listed above can only be true if 2 conditions are sufficed
- lim g(x) = L (limit of g(x) actually needs to exist) x -> a
- function “f” needs to be continuous at L
Example: lim f(g(x)) x -> -3
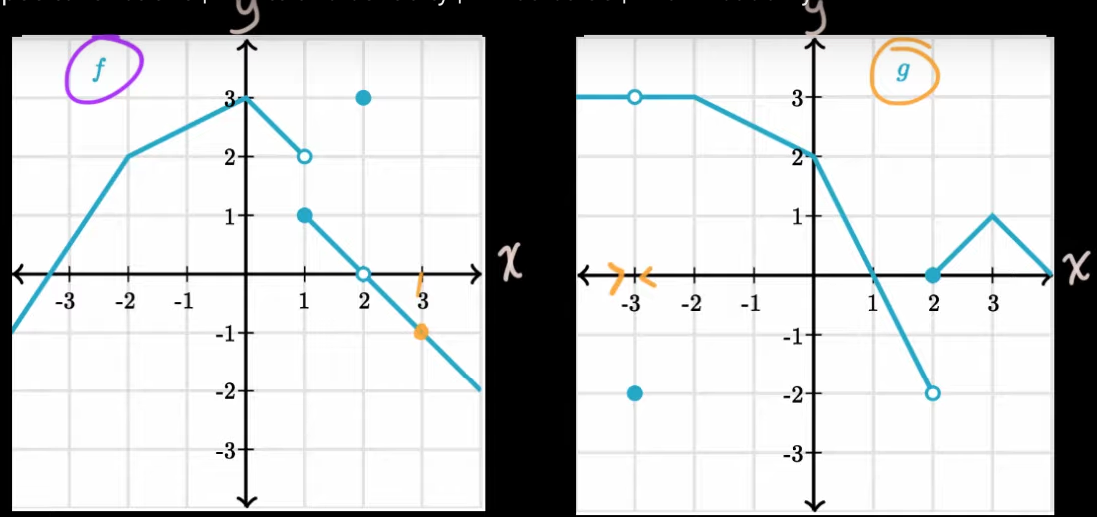
From the f(x) and the g(x) graphs above we can tell that
- lim g(x) = 3 Limit exists! x -> -3
- f(x) is continuous at x = 3
Both of are conditions have been sufficed does our condition hold true?
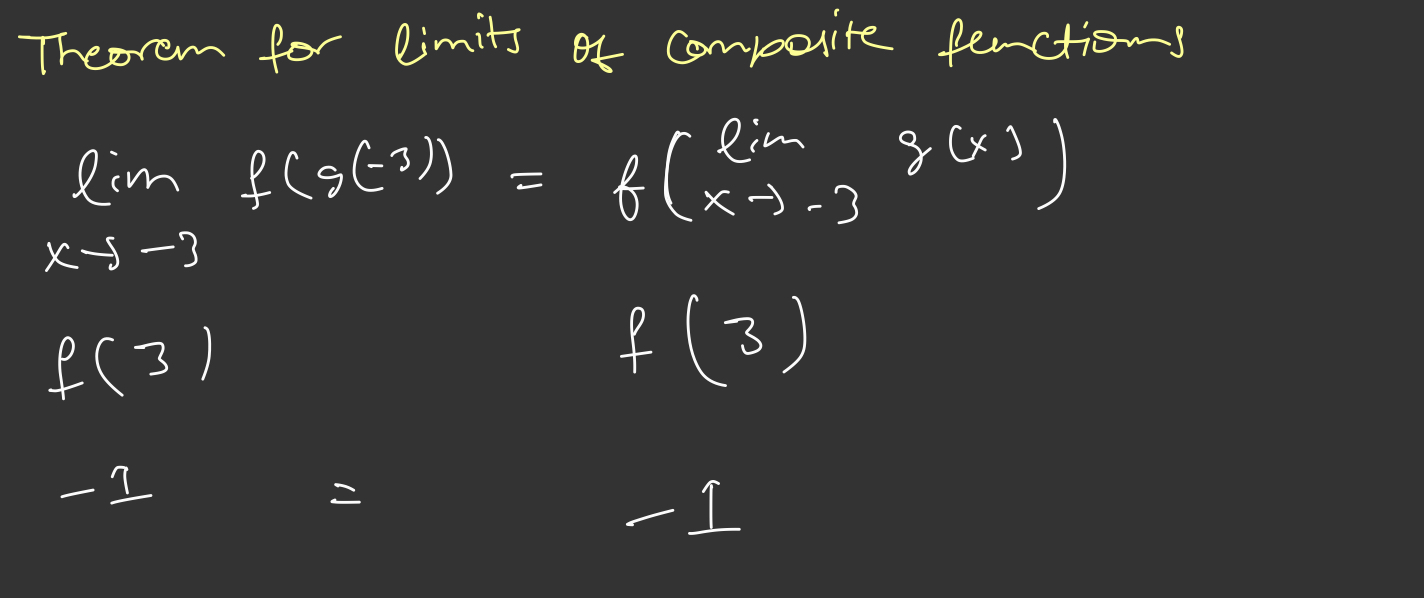
When conditions aren’t met
When both conditions aren’t met you cannot apply the theorem but that doesn’t mean the limit doesn’t exist