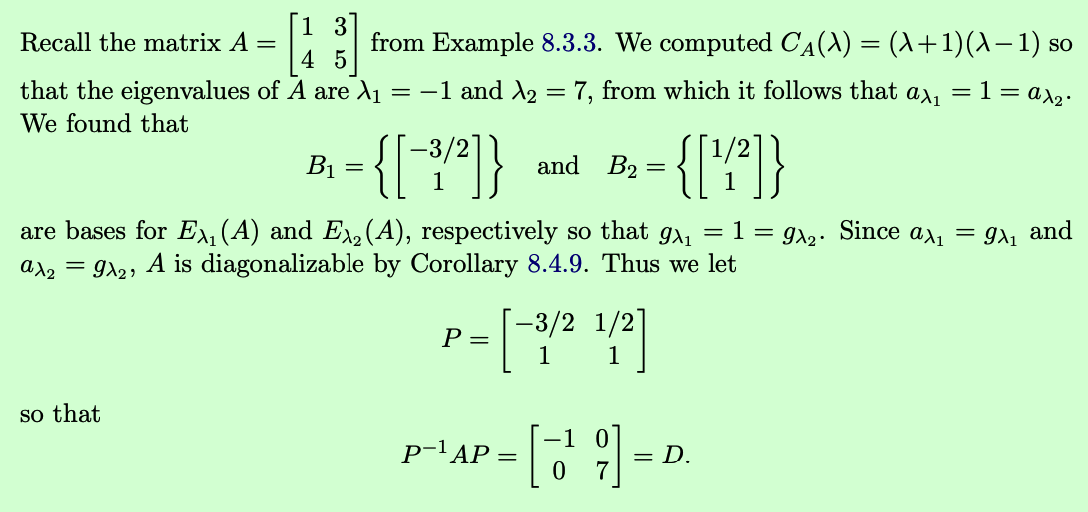Diagonalization

[!Definition 8.4.1]

A matrix D = $[d_{ij}]\in M_{nxn}(\mathbb{R})$ is a diagonal matrix if $d_{ij}=0$ for all $i\ne j$. In this case, we may write $D=diag(d_{11},\dots ,d_{nn})$

[!Definition 8.4.4]

A matrix $A\in M_{nxn}(\mathbb{R})$ is diagonalizable if there exists an invertible matrix $P\in M_{nxn}(\mathbb{R})$ and a diagonal matrix $D\in M_{nxn}(\mathbb{R})$ so that $P^{-1}AP=D$. In this case, we may say that P diagonalized A to D

[!Corollary 8.4.9]

Let $A\in M_{nxn}(\mathbb{R})$ and assume that none of the eigenvalues of A are non-real. Then A is diagonalizable if and only if $a_{\lambda }=g_{\lambda }$ for every eigenvalue $\lambda$ of A