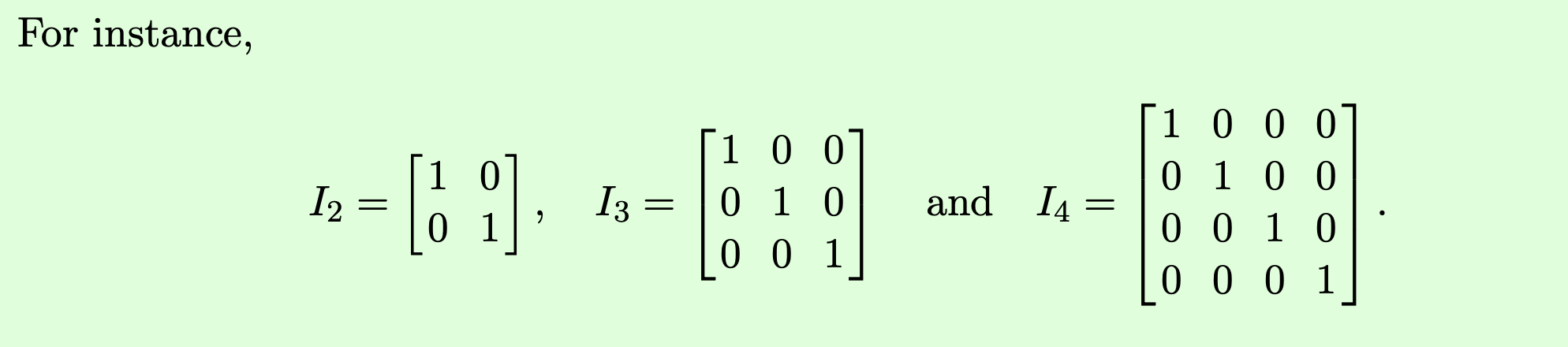Matrix-Vector Product

Introduced to in Math 115

[! Definition 3.2.2 Matrix-Vector Product]

Let A = [] and = . Then the vector A is defined

A =

[! Matrix Equality Theorem]

Let A, B . If A = B for every , then A = B

[! Properties of Matrix Vector Product]

Let A, B and c Then

a) A() =

b) A(c) = c(A) = (cA)

c) (A + B) = A

The n x n identity matrix, denoted by I (or I or just I if the size is clear) is the square matrix of size n n with (I) = 1 for i = 1, 2, , n and zeros elsewhere