SE212 - Propositional Logic

• $\models$ (logical implication / entailment)
• $⟺$ (logical equivalence)

Brackets and Precedence

• $\neg$ Highest
• $\wedge$
• $\vee$
• $\Rightarrow$
• $\iff$ Lowest

Binary logical connectives are right associative

Eg. $a\vee b\vee c$ means $a\vee (b\vee c)$

• Boolean Valuations- prime propositions are assigned truth values (T or F) and in all Boolean valuations
• Tautology / Valid - Propositional formula is a tautology or valid if [P] = T for all Boolean valuations
• Contradiction / Falsehood - Propositional formula is a contradiction or a falsehood if [A] = F for all Boolean valuations
• Contingent Formula - a formula that’s neither a tautology nor a contradiction
• Consistent - Collection of formulas are consistent if there is a Boolean valuation in which all the formulas are T

Transformational Proof §

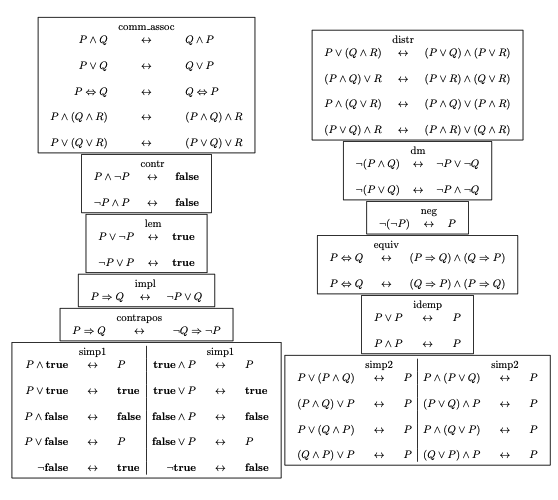
Two rules are used implicitly in transformational proofs:

1. Rule of substitution - Substituting an equivalent formula for a subformula
2. Rule of transitivity - If $P\leftrightarrow Q$ and $Q\leftrightarrow R$, then $P\leftrightarrow R$. This rule connects the steps of the proof

Rules of thumbs for transformational proofs:

1. Eliminate implication and if and only if using the law of implication, the law of equivalence, and contrapositive law backwards
2. Simplify as soon as you can (simp1, simp2, idemp, neg, contr, lem)
3. Use the various kinds of simplification backwards to prepare for using distributivity

• Conjuctive Normal Form (CNF) - Conjunction of one or more clauses, where a clause is a disjunction of literals or single literal
  • How to convert:
    • Remove all implications and iff using laws
    • If formula contains any negated compound formulas remove the neg or use DM to push the negation in
    • Once a formula with no negated compound subformulas is found, use distributivity laws
      • $A\vee (B\wedge C)\leftrightarrow (A\vee B)\wedge (A\vee C)$
      • $(A\wedge B)\vee C\leftrightarrow (A\vee C)\wedge (B\vee C)$
    • Simplify
• Disjunctive Normal Form (DNF) - Disjunction of one or more clauses, where a clause is a conjunction of literals or a single literal
  • Remove all implications and iff using laws
  • If formula contains any negated compound formulas remove the neg or use DM to push the negation in
  • Once formula with no negated compound subformulas is found, use distributivity laws
    • $a\wedge (b\vee c)\leftrightarrow (a\wedge b)\vee (a\wedge c)$
    • $(a\vee b)\wedge c\leftrightarrow (a\wedge c)\vee (b\wedge c)$
  • Simplify

Natural Deduction §

Natural deduction is a proof theory for proving the validity of an argument in propositional logic

Natural deduction is a form of forward proof

Forward Proof - Write down premises and then add formulas to the proof that we can deduce from lines already in the proof until we reach the conclusion

Subordinate Proofs - Start by choosing a formula that we can assume is true within the subproof, then we see what we can prove based on that assumption and any prev deduced formulas

3 proof rules use this approach:

• Conditional proof (imp_i)
• Proof by contradiction (raa)
• Case analysis (raa)